LEXIQUE :

Base de sondage :

Liste numérotée ( de 1 à N) des N individus d'une population, dans laquelle on veut par sondage extraire un échantillon.

Biais : (Sans)

Un estimateur d'un paramètre θ est sans biais si son espérance est égale à θ.

Par exemple la moyenne 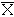calculée sur un échantillon aléatoire simple est un estimateur sans biais de la moyenne m de la population.

Sinon, le biais d'un estimateur est la valeur de E ( ) - θ.

Un biais positif signifie que l'estimation, en moyenne, surestime θ, alors qu'un biais négatif le sous-estime.

Convergence de la loi binomiale vers la loi normale :

a) de la loi binomiale vers la loi de Poisson :

Si X suit B ( n , p ), n → ∝, p → 0, np → λ, alors la loi de X se rapproche de P ( λ ).

(en pratique, si n > 50 et p < 0.1, on peut remplacer B ( n , p ) par P ( n p ) )

b) de la loi binomiale vers la loi normale :

Si X suit B ( n , p ), quand n → ∝, tend vers la loi N (0, 1)

(en pratique, si n p > 18 et p assez proche de 0.5, on peut remplacer la loi de X par N (np ; )

c) de la loi de Poisson vers la loi normale :

Si X suit P( λ ), tend, quand λ → ∝, vers la loi N (0,1) (en pratique, si λ > 18, on peut remplacer la loi de X par N ( λ ))

Convergence de la loi hypergéométrique vers la loi binomiale :

Convergence de la loi hypergéométrique vers la loi binomiale :
si n tend vers l'infini, la loi H ( n , m , p ) tend vers la loi B ( m , p ), c'est-à-dire que lorsqu'on effectue un tirage dans une grande population, il importe peu que ce tirage se fasse avec ou sans remise (en pratique, on considèrera que la population est "grande" lorsque l'échantillon représente moins de 10 % de cette population : m / n < 0.1 )

Convergence d'un estimateur : (Estimateur convergent)

Un estimateur d'un paramètre θ est convergent s'il tend, lorsque la taille n de l'échantillon tend vers l'infini, vers le paramètre θ à estimer.

Ceci est réalisé en particulier lorsque est sans biais et que sa variance tend vers 0 quand n tend vers l'infini.

(Dans ce cas on dit parfois aussi que est absolument correct)

Ecart-type :

L'écart-type d'une variable aléatoire numérique X, noté σ ( X ), est la racine carrée de la variance.

L'écart-type s'exprime dans la même unité que X ; c'est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".

Exemple : si X suit une loi normale, la probabilité pour que X soit compris entre E ( X ) - 2 σ ( X ) et E ( X ) + 2 σ ( X ) est à peu près de 0.95.

Echantillon :

Partie d'une population, obtenu par sondage : échantillon de 1000 personnes parmi les habitants d'une ville, ou de 50 lampes électriques d'une marque donnée, ou de 10 entreprises d'un secteur industriel, ou de 100 votants lors d'une élection, etc...

Echantillon aléatoire simple : (ou Echantillonnage)

Echantillon obtenu par tirages équiprobables et indépendants de n éléments d'une population : chaque individu a la même probabilité d'être tiré, et ceci de façon indépendante d'un individu aux suivants (tirage dit "avec remise").

Ce terme désigne aussi :
- une suite de n variables aléatoires indépendantes de même loi de probabilité ( X₁, X₂ , ... , X_n )
- la réalisation de cette suite de variables : ( x₁, x₂ , ... , x_n )

Par exemple l'échantillon peut être 100 personnes choisies au hasard parmi la population d'une ville, ou les salaires de ces 100 personnes, ce peut être de même un échantillon de 50 pièces fabriquées par une machine, ou les diamètres de ces 50 pièces, ou les poids de ces 50 pièces, etc...

Echantillon stratifié optimal :

Un échantillon stratifié est optimal s'il comprend un nombre d'individus par strate rendant la variance de l'estimateur minimale.

Ce nombre est proportionnel au produit du nombre d'individus par strate dans la population et de l'écart-type dans la strate.

Echantillon stratifié représentatif :

Un échantillon stratifié est représentatif s'il comprend un nombre d'individus par strate proportionnel au nombre d'individus par strate dans la population.

Espérance :

L'espérance (mathématique) d'une variable aléatoire numérique X, appelée aussi parfois par abus de langage moyenne de X, est la valeur que l'on peut espérer obtenir, en moyenne, en réalisant X.
Elle est notée E ( X ).

a) dans le cas d'une variable X discrète, de loi de probabilité définie par les x_i et les p_i, c'est la moyenne des x_i, pondérée par les p_i

b) dans le cas d'une variable X continue, de fonction de densité f, c'est l'intégrale, sur l'intervalle des valeurs de X, de la fonction x f ( x ) :

E ( X ) = ∫ x f ( x ) d x

Estimateur :

Variable aléatoire, fonction de variables d'échantillon X₁, X₂, ... , X_n dont la réalisation est une estimation (c'est-à-dire une valeur approchée) d'un paramètre θ inconnu de la population.

Par exemple : = est un estimateur de m,
moyenne de la population ( m = E ( X ) ). Sa réalisation est , moyenne calculée sur l'échantillon.

Estimation par intervalle :

On dit que l'on procède à une estimation par intervalle d'un paramètre θ lorsqu'on détermine un intervalle de confiance pour θ.

Estimation ponctuelle :

C'est une valeur approchée du paramètre θ inconnu d'une population, calculée à partir d'un échantillon.

C'est en fait la réalisation d'une variable aléatoire , estimateur de θ.
Par exemple le % de votants obtenus pour M. Truc lors d'une élection, sur 1 000 bulletins dépouillés au hasard, est une estimation du % de voix de M. Truc.

Facteur d'exhaustivité :

C'est le nombre par lequel il faut multiplier la variance de ( ou de F ) lorsqu'on a un tirage exhaustif, et non pas sans remise (N est la taille de la population, n celle de l'échantillon).

Ce nombre étant inférieur à 1, cela signifie que la variance est plus faible lorsque le tirage se fait sans remise.

Lorsque la population est très grande (N beaucoup plus grand que n), le facteur d'exhaustivité est négligeable (presque égal à 1).

Fonction de répartition empirique :

Fonction réelle calculée sur un échantillon de taille n qui, à tout réel x, associe la proportion d'éléments de l'échantillon ≤ x.

Par exemple F ( x ) peut être le % d'ampoules de durée de vie inférieure ou égale à x, sur un échantillon de 500 ampoules.

(Alors que la fonction de répartition théorique de la durée de vie d'une ampoule de ce type est la probabilité que sa durée de vie soit inférieure ou égale à x).

Fractile :

Le fractile (ou quantile) d'ordre p ( p compris entre 0 et 1 ) d'une variable aléatoire X, est la valeur x telle que P ( X < x ) = p.

Par exemple : le fractile (ou quantile) d'ordre 0.975 de la loi N ( 0 , 1 ) est égal à 1.96 puisque Π ( 1.96 ) = 0.975 ( Π étant la fonction de répartition de N ( 0 , 1 ).

Individus :

Ce sont les éléments d'une population statistique : chaque habitant d'une ville, chaque commune d'un pays, chaque pièce fabriquée par une machine, etc..., est un individu statistique [ou unité statistique] sur lequel on peut effectuer une enquête ou des mesures.

Intervalle bilatéral : (de confiance)

C'est un intervalle de confiance comprenant deux bornes finies, de la forme [ θ₁, θ₂ ] :

P ( θ₁ < θ < θ₂) = 1 - α (niveau de confiance)

Intervalle bilatéral symétrique en probabilité :

Intervalle de confiance bilatéral de niveau 1 - α :

P ( θ₁ ≤ θ ≤ θ₂ ) = 1 - α , où θ₁ et θ₂ sont tels que

P ( θ < θ₁ ) = P ( θ > θ₂ ) = α / 2

Intervalle de confiance : (de niveau 1 - α)

Un intervalle de confiance de niveau 1 - α pour un paramètre inconnu θ d'une population est un intervalle tel que la probabilité pour que θ appartienne à cet intervalle est 1 - α. Les bornes de cet intervalle se calculent à partir d'un échantillon.

Par exemple, si M. Truc obtient 40 % des voix sur un échantillon aléatoire simple de 1000 votants, on peut dire, avec une probabilité de 0.95, que le % de votants pour M. Truc se situe entre 37 % et 43 %.
[37   43] est un intervalle de confiance de niveau 0.95 pour le % de votants pour M. Truc.

Intervalle unilatéral : (de confiance)

C'est un intervalle de confiance comprenant une seule borne finie, de la forme

[ θ₁, + ∝ [   :   P ( θ ≥ θ₁ ) = 1 - α

ou

] - ∝ , θ₂ ]   :   P ( θ ≤ θ₂ ) = 1 - α

1 - α est le niveau de confiance de l'intervalle.

Loi de Bernoulli :

C'est la loi d'une variable aléatoire X prenant les valeurs 1 et 0 avec les probabilités :

P ( X = 1 ) = p , P ( X = 0 ) = 1 - p.

Exemple : tirer à "pile ou face", tester une pièce dans la production d'une machine (pièce défectueuse ou pas), ...

Loi binomiale :

C'est la loi de X = nombre de réalisations d'un événement dans une suite de n épreuves indépendantes où l'événement a la probabilité p de se produire.

X est la somme de n variables de Bernoulli indépendantes de même p :

= { 0, 1, 2, ..., n} , P ( X = k ) = 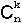p^k ( 1 - p )^n-k   ,   ∀ k ∈ { 1, 2, ..., n }

E ( X ) = n p

V ( X ) = n p ( 1 - p )

Exemples :
- nombre de "pile" obtenu en lançant 10 fois une pièce : B ( 10 ; 0.5 )
- nombre de pièces défectueuses trouvées parmi 100 ..

Loi hypergéométrique :

C'est la loi du nombre X d'individus possédant un certain caractère, lors du tirage sans remise de m individus parmi n, dont une certaine proportion p a ce caractère :

P ( X = k ) = 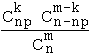, k ∈ { 0, 1, 2, ... , m }

(si le tirage s'effectue avec remise, X suit une loi binomiale B ( m , p ) )

Si n est grand ( m / n < 0,1), la loi de X est à peu près B ( m , p ).

Loi des grands nombres :

Elle peut s'exprimer de deux façons :

1) Lorsqu'on effectue un échantillonnage aléatoire simple, la fréquence d'apparition d'un événement F tend, quand la taille n de l'échantillon tend vers l'infini, vers la proportion p dans la population-mère.
Par exemple, si l'on pouvait jouer indéfiniment à "pile ou face" avec une pièce bien équilibrée, le pourcentage de "pile" obtenu tendrait vers 50 %.

2) De même, la moyenne d'une variable sur un échantillon aléatoire simple tend, quand n tend vers l'infini, vers la moyenne dans la population.

Par exemple, la taille moyenne de n enfants de 10 ans pris au hasard dans la population française tend, si n tend vers l'infini, vers la taille moyenne de tous les enfants français de 10 ans.

Loi du khi-deux :

Une variable aléatoire X suit une loi du 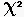à n degrés de liberté si X est égale à la somme des carrés de n variables aléatoires indépendantes de loi normale centrée réduite. Cette loi est tabulée (cf. Tables).

Loi Normale (ou de Gauss) :

a) X suit une loi normale centrée réduite, notée N (0, 1) si sa fonction de densité est :

f ( x ) = e^-x²/2

Sa fonction de répartition se lit dans une table.

b) X suit une loi normale de paramètres m et σ, notée N ( m , σ ), si sa fonction de densité est :

f ( x ) = e^{-(x-m)²/2 σ²}

suit alors une loi normale centrée réduite.

On dit aussi que X suit une loi de Gauss ou une loi de Laplace-Gauss

Loi de Poisson :

C'est la loi d'une variable X à valeurs dans N telle que

P ( X = k ) = , k ∈ N

Si X suit une loi binomiale B ( n , p ) avec p faible ( < 0,1 ),
et n grand ( n > 50 ), la loi de X est très proche de la loi P ( n p ).

Exemple : nombre de pièces défectueuses dans un grand échantillon de bonne qualité.
C'est aussi la loi du nombre d'événements se produisant pendant une période T, ou sur une distance T, et ne dépendant que de T, les événements étant indépendants, et non simultanés.

Exemple : nombre d'accidents par an sur une route, nombre de défauts par mètre de tissu, nombre d'appels téléphoniques reçus à un standard pendant une journée.

Si X suit une loi P ( λ ), E ( X ) = V ( X ) = λ

Loi de Student :

Une variable aléatoire X suit une loi de Student à n degrés de liberté si X est de la forme

, où U et Y sont indépendantes,
U de loi N (0, 1) et Y de loi 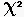( n ).

Cette loi est tabulée (cf. Tables)

Marge d'erreur :

Lorsque les bornes d'un intervalle de confiance bilatéral symétrique en probabilité d'un paramètre θ sont de la forme : ± e ,
e est appelé marge d'erreur.

Par exemple : e = u est la marge d'erreur sur l'estimation d'une proportion inconnue p par f, proportion dans l'échantillon.

P ( θ ∈ [ - e ; + e ] ) = 1 - α

Méthodes empiriques :

Méthodes résultant d'expérimentations pratiques, et non issues d'une théorie, telle la théorie des probabilités et statistique mathématique.

Moyenne empirique : Moyenne (variance, écart-type) empirique

C'est la moyenne (variance, écart-type) calculée sur les valeurs obtenues dans l'échantillon. C'est en fait la réalisation d'une variable aléatoire :

la moyenne empirique = est la réalisation de

= , que l'on appelle aussi moyenne empirique.

Nombres au hasard : (Table de nombres au hasard)

Liste de chiffres, de 0 à 9, telle que chacun soit obtenu avec la même probabilité (on a une chance sur 10 d'avoir le 0, une chance sur 10 d'avoir le 5, etc...), et de façon indépendante : la connaissance d'un certain nombre de chiffres de la table n'apporte aucune information sur les autres.

Nombres pseudo-aléatoires : (Générateur de nombres pseudo-aléatoires)

Obtention par un procédé informatique de nombres tirés au hasard, de façon équiprobable et indépendante (en fait ces nombres sont générés par une fonction, mais tellement complexe que tout se passe comme s'ils étaient indépendants les uns des autres).

Population :

Ensemble bien défini de personnes, ou d'objets, sur lesquels on effectue des mesures (population formée des habitants d'une ville, ou des communes d'un pays, ou des entreprises d'une région, ou des pièces fabriquées par une machine, ou des boîtes de conserves d'un magasin, etc...).

Les mesures peuvent être effectuées sur la population toute entière, ou seulement sur une partie d'entre elle, appelée échantillon.

Population-mère : (d'un échantillon)

Population dont est issu l'échantillon.

Quantile :

Le quantile (ou fractile) d'ordre p ( p compris entre 0 et 1) d'une variable aléatoire X, est la valeur x telle que P ( X < x ) = p.

Par exemple : le quantile (ou fractile) d'ordre 0.975 de la loi N (0, 1) est égal à 1.96 puisque Π( 1.96 ) = 0.975 ( Π étant la fonction de répartition de N (0, 1)).

Sondage :

Mode d'obtention d'un échantillon, issu d'une population donnée.

Sondage à probabilités inégales :

Choix d'un échantillon dans une population, de telle sorte que les individus n'aient pas tous la même probabilité d'être choisis.

Sondage stratifié : (ou échantillonnage stratifié)

Méthode de sondage dans une population subdivisée en plusieurs sous-populations (tranches d'âges par exemple) : on choisit un sous-échantillon dans chacune des sous-populations, pour obtenir un échantillon stratifié : choix au hasard d'un nombre donné d'individus par tranche d'âge par exemple.

Strates :

Si une population est partitionnée en un certain nombre de sous-populations distinctes (hommes - femmes par exemple, ou tranches de salaires, ...), ces sous-populations sont appelées des strates.

Taille : (d'un échantillon)

Nombre n d'éléments de l'échantillon.

Par exemple un échantillon de 1000 électeurs est un échantillon de taille 1000.

Taux de sondage :

Proportion (ou pourcentage) de la population totale échantillonnée lors d'un sondage sans remise.

Par exemple : Si l'on choisit, sans remise, un échantillon de 5 000 individus dans une population en comportant 100 000, le taux de sondage est :

= 0.05 , soit 5 %.

Tirage avec remise :

Se dit d'un tirage dans lequel on peut obtenir plusieurs fois le même élément : un objet est choisi au hasard dans la population, puis un deuxième toujours dans la même population (comprenant donc aussi le 1^er choisi), etc...

Tout se passe comme si on remettait chaque élément choisi dans la population avant d'en choisir un autre.

Tirage sans remise : (ou tirage exhaustif)

Se dit d'un tirage dans lequel on ne peut obtenir plusieurs fois le même élément. Par exemple un tirage sans remise de 5 cartes dans un jeu de 32 cartes consiste à choisir 5 cartes différentes parmi les 32.

Un échantillon construit par ce procédé comprend des variables
X₁ , X₂ , ... , X_n non indépendantes.

Théorème central limite :

Si X₁ , X₂ , X₃ , ... , X_n sont des variables aléatoires indépendantes, de même loi de probabilité, d'espérance µ et de variance σ², la loi de probabilité de

tend, quand n → ∝ , vers la loi normale centrée réduite.

Variables : (statistiques)

C'est ce qui peut être mesuré sur les individus statistiques, éléments d'une population : âge des habitants d'une ville, leur salaire, leur profession, dimensions des pièces mécaniques fabriquées par une machine, taille des entreprises d'un secteur industriel, etc..., sont des variables statistiques.

Variable aléatoire :

Une variable aléatoire X est une grandeur qui peut prendre différentes valeurs avec différentes probabilités ; l'ensemble des valeurs que peut prendre X est noté .

X est en fait une application qui, à toute issue d'une expérience aléatoire, associe un élément de .

Selon la nature de , X sera une variable qualitative, numérique discrète ou numérique continue.

Variance :

La variance d'une variable aléatoire numérique X, notée V ( X ), est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".

V ( X ) = E [ ( X - E ( X ) )² ] ( ici E signifie l'espérance )

On a aussi : V ( X ) = E ( X² ) - [ E ( X ) ]²,

formule qui peut se lire : la variance est égale à l'espérance du carré moins le carré de l'espérance.

La racine carrée de la variance est l'écart-type.

Variance minimum : (ou efficace)

Un estimateur est dit de variance minimum, s'il a la variance la plus faible.

Si et sont deux estimateurs sans biais d'un même paramètre θ ,

sera dit plus efficace que si V ( ) < V ( ).